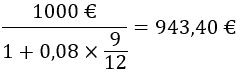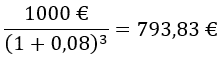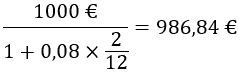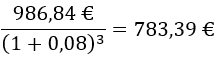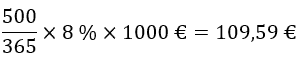Diskonttaus ja viivästyskorkojen laskeminen
Diskonttauksella tarkoitetaan tulevaisuudessa tapahtuvan maksun nykyarvon laskemista. Laskujen rahoituksessa diskonttaus ilmenee siten, että pitkissä laskujen maksuehdoissa rahoituksen hinta on lyhyempiä suurempi.
Diskonttauksen kaava, kun
- maksuaika on enintään vuoden mittainen
- diskonttokorkona käytetään vuotuista korkoa
- maksu tapahtuu yhdessä erässä
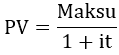
PV = maksun nykyarvo (present value)
i = vuotuinen korkokanta (interest)
t = maksuaika/korkojakso (time)
Esimerkki 1
Yritys saa 1 000 euron suorituksen yhdeksän kuukauden päästä. Mikä on suorituksen nykyarvo, kun korkokantana käytetään 8 %:n vuosikorkoa?
Diskonttauksen kaava, kun
- maksuaika on useamman kokonaisen vuoden mittainen
- diskonttokorkona käytetään vuotuista korkoa
- maksu tapahtuu yhdessä erässä
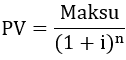
n = maksuaika kokonaisina vuosina
Esimerkki 2
Yritys saa 1 000 euron suorituksen tasan kolmen vuoden päästä. Mikä on suorituksen nykyarvo, kun korkokantana käytetään 8 %:n vuosikorkoa?
Esimerkki 3
Yritys saa 1 000 euron suorituksen 38 kuukauden päästä. Mikä on suorituksen nykyarvo, kun korkokantana käytetään 8 %:n vuosikorkoa?
Maksuaika on nyt yli vuoden, mutta ei kuitenkaan tasavuosia, joten diskonttaus tehdään kahdessa vaiheessa:
Ensin diskontataan kaksi viimeistä kuukautta:
Sitten diskontataan 36 kuukautta eli kolme vuotta:
Diskonttauksen laskentakaavat pääomittavat kunakin vuonna kertyneen koron kasvamaan korkoa korolle seuraavan vuoden alusta alkaen.
Viivästyskorkojen laskeminen
Viivästyskorkojen laskennassa käytetään kohtuussyistä ns. yksinkertaista korkolaskua, jolloin kunakin vuonna kertyneitä viivästyskorkoja ei pääomiteta kasvamaan korkoa korolle seuraavana vuonna. Viivästyskorkoja koskeva korkoa korolle -kielto (anatocismuksen kielto) periytyy jo antiikin ajan roomalaisten kahdentoista taulun laista (lex duodecim tabularum) noin vuodelta 450 ennen ajanlaskun alkua.
Esimerkki 4
Yritys maksaa 1 000 euron laskun 500 päivää myöhässä. Mikä on viivästyskoron määrä 8 %:n vuosikorolla?